Bayesian Statistics is Not Esoteric! It’s Groovy!

This past weekend, I attended an introductory talk and workshop on Bayesian statistics at Vassar given by Indian University professor John Kruschke. Before I go on, I’d like to make three points very clear:

1) This post isn’t so much about evolutionary clinical psych per se, but it has relevance for anyone doing any type of research which uses statistics.

2) Going into this workshop, my statistical skills and knowledge set would rank about a 4.5 on a 10 point scale, with 10 being a statistical genius—which brings me to my third point:

3) John Kruschke is an extraordinarily good instructor, and if you get the chance, you should see him speak, buy his highly-Amazon-rated book (the book’s lowest rating is 4 stars and is titled “Amazing”), and/or read his papers on Bayesian stats…I understood almost every word he said, even though I’m only a stats novice, when it comes right down to it. I found Bayesian statistics to be a lot simpler than I had expected, in large part due to Dr. Kruschke’s style.

So….Bayesian statistics is an alternate approach to traditional Null Hypothesis Significant Testing (NHST) which is the standard method that everybody learns when first learning statistics. Almost everybody uses it when they analyze data and publish papers, making it in essence the standard way statistics has been done ever since Ronald Fisher expounded it in the early 20^th century: calculate a statistic (a mean, for example) from your model that may or may not represent the population mean…then, based on sample size, method of data collection, and a number of other factors, you come up with a p (significance) value to decide whether to reject the null (i.e., conclude that the populations you are comparing are different), or not (i.e., fail to conclude that there is a difference).

The problem with NHST is that the p value is a goalpost that can be too easily moved, both unintentionally and intentionally, depending on the researcher’s goals, aims, collection/analysis methods, and agenda. Since the decision to reject or accept a null hypothesis based on significance is thought of as a binary decision, it is dismaying easily to get diametrically opposite results (accept vs. reject null hypothesis) with a single set of data.

In a simple example demonstrated by Dr. Kruschke, the critical value in a t-test can shift depending on whether you intend to collect data until you reach a particular N (number of subjects) OR if you intend to collect data until a particular time (e.g., Friday at 5:00pm). (I think the reason for this is that degrees of freedom are calculated differently in the latter scenario, but I could be wrong.) So with a single data set and a single t value, you can either reject or accept the null! Which is the correct answer??

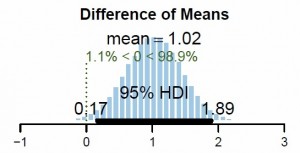
Enter Bayesian statistics, which is based on distributions of probability (also known as credibility within the field). Rather than a statistic and a significance value (the latter of which is, again, fickle) as in NSHT, the output of a Bayesian analysis (see Figure 1) is a value (in this example, a difference of means between groups A and B, 1.02) which purports to describe the population parameter, and a probability distribution that describes a range of likelihoods of similar values (shown by the histogram). The high-density area (HDI) is the range of values in which there is a 95% of the true mean falling. You can see that zero lies well outside the HDI, and the green numbers tell us that there is a 98.9% chance that the true difference of means is greater than 0. Based on this, we can make a probabilistic decision to reject or accept the null (rejection is obviously the more probable decision), but the point is, the findings are what they are…anybody running this analysis with this data will get the same outcome, which is more than can be said for the p value.

That’s it! Look how simple and elegant, yet information-rich this result is compared to an NHST result. The HDI is reminiscent of a confidence interval in NHST, yet a CI has no probabilistic distributional information about the values within, whereas the HDI does. NHST is also dependent on assumptions of normality and very sensitive to outliers. It also relies on confusing concepts of sampling distributions which Bayesian approaches do not need. Further, Bayesian stats utilizes a prior probability, which the current data updates to result in a posterior credibility; purposely vague priors (like uniform distributions) are often used, but if there is a theoretical basis for it, a prior can be used which incorporates probabilistic information from prior findings. This type of analysis would make it a lot less easy to find a significant effect for pseudo-scientific/paranormal phenomena, considering the thousands of negative prior results that could be loaded into a current analysis of, say, psi effects (see Wagenmakers, et al.)

In fact, there’s a whole litany of reasons why Bayesian stats is superior to NHST. It’s the way of the future, if Bayesians are to be believed. So why hasn’t it caught on yet?

The most probable answer, in my opinion, is that the best way to do Bayesian analysis right now is with the statistical language R, which has a sickeningly steep learning curve for those not used to programming languages or syntax. Here’s part of the code for a One-Way ANOVA:

Compared to even the quasi-intuitive menus and graphical interface of SPSS, it’s enough to give anyone a case of the vapors. By all accounts, R is much more flexible and versatile than any of the existing stats softwares, but it really doesn’t have mass appeal right now. In a few years, somebody will have put together a menu-based graphic user interface to sit over R, but for now, the best we have is RStudio, which is free to all and has a large online user support network, but still necessitates learning the R language.

There’s also the issue of institutional inertia; most current publications utilize standard NSHT. If/when more people start using Bayesian stats, there will be a bandwagon effect, especially if journals actively encourage Bayesian approaches.

By the way, there were a couple of resistant audience members in the back of the room who weren’t convinced that Bayesian methods were better, openly challenging Kruschke in the middle of his lecture (only ten minutes in, rather than waiting for the Q&A, which I thought demonstrated egregiously poor decorum) and muttering like Statler and Waldorf to each other as he proceeded. My inference was that some people actively resist Bayesian approaches because they either feel NHST is superior or they are direct descendents of Ronald Fisher. Feel free to comment and explain yourself if you’re in this camp.

For now, I’m going to predict that eventually, Bayesian stats will be easy enough for everyone to use…in the meantime, I encourage everyone to at least look into it.